一个国家为了防御敌人的导弹袭击，开发了导弹拦截系统。但是这个导弹拦截系统有个缺陷：虽然它的第一弹可以达到任意高度反导弹系统需要雷达吗?，但是后面的每一个弹都不能比前一个高。一天，雷达探测到一枚来自敌国的来袭导弹。由于该系统仍处于试验阶段反导弹系统需要雷达吗?，只有一个系统，因此可能无法拦截所有导弹。
依次输入导弹飞行高度（雷达给出的高度数据为不大于30000的正整数），计算该系统最多可以拦截多少枚导弹，需要多少套该导弹拦截系统至少拦截所有导弹。
输入
1行，数个整数( number ≤ 100000）
输出
2行，每行是一个整数，第一个数字表示该系统最多可以拦截多少枚导弹，第二个数字表示该导弹拦截系统至少应该配备多少套拦截所有导弹。
样本输入
389 207 155 300 299 170 158 65
样本输出
6
2
问题：给定一个序列，找出可以用来表示它的降序子序列的最小数量和最长降序子序列的长度
思路：先用O(n^2)的朴素解求最长降序子序列的长度，然后根据这个解改成最长降序子序列。遍历每个元素时，有两种可能，要么接收一个已有的降序子序列，要么打开一个新的子序列。正确的贪心应该是接收大于当前元素的最小值。如果没有，则打开一个新的。这就是找到最大值。最老的子序列。
#include
using namespace std;
typedef pairPII;
typedef long long ll;
int ans,sum;
const int N=1e5+10;
int f[N];
int d[N];
int g[N];
int n;
int main()
{
n=1;
string line;
getline(cin, line);
stringstream ssin(line);
while (ssin >> d[n]) n ++ ;
n--;
int sum=0;
for(int i=1;i
if(d[j]>=d[i])
f[i]=max(f[i],f[j]+1);
sum=max(sum,f[i]);
}
int cnt=0;
for(int i=1;i<=n;i++)
{
int k=0;
while(k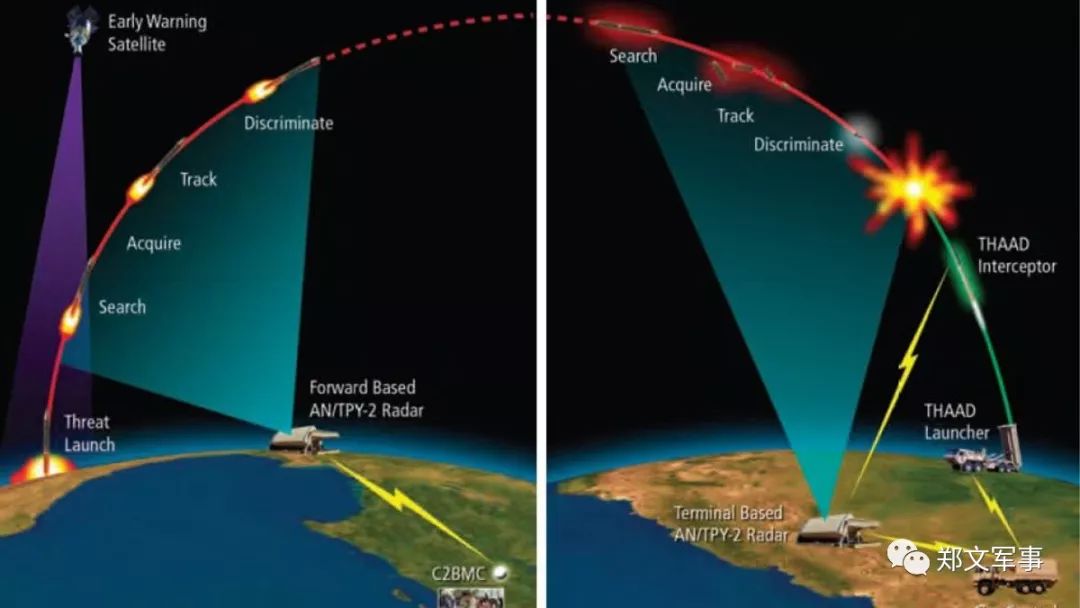
g[k]=d[i];
if(k>=cnt) cnt++;
}
cout< 想法：
